قائمة الانتظار Data Structure and Algorithms – Queue

-

قائمة الانتظار Queue: هي بنية بيانات مجردة abstract data structure. على عكس stacks، فإن queue مفتوحة من طرفيها. حيث يتم استخدام أحد الطرفين دائمًا لإدخال البيانات (enqueue) والطرف الآخر يستخدم لإزالة البيانات (dequeue). 

يتم تطبيق منهجية First-In-First-Out (FIFO)، بمعنى آخر: العنصر الأول هو اول عنصر يتم الوصول اليه. 

أيضا منهجية Last-In-Last-Out (LILO). تطبق على هذا النوع حيث اخر عنصر تم إدخاله سيكون اخر عنصر تم خروجه.

من الأمثلة الواقعية على queue. طوابير الانتظار في خط واحد. مثلا خط لخدمة السيارات مكون من مسار واحد وباتجاه واحد، اكيد في هذه الحالة سيتم الوصول الى اول سيارة موجودة أولا.

كما هو الحال في stacks، يمكن أيضًا تنفيذ قائمة انتظار queue باستخدام المصفوفات Arrays والقوائم المرتبطة Linked-lists والمؤشرات Pointers وStructures. 

لا يمكنك استخدام قائمة الانتظار Queue لعمليات LIFO ولا يمكنك تخزين البيانات الهرمية فيها hierarchical data. يتم تنفيذ قوائم الانتظار بطريقتين:

• استخدام المصفوفات Arrays
• استخدام القوائم المرتبطة Linked-List.

لكل منها مزاياها وعيوبها.

استخدام المصفوفات Array له قيود على المساحة space limitations وبالتالي سعة محدودة limited capacity.

لحل مشكلة السعة نستخدم Linked-list، لكنه بطيء.

في هذا الدرس سنستخدم مصفوفة أحادية البعد one-dimensional array.

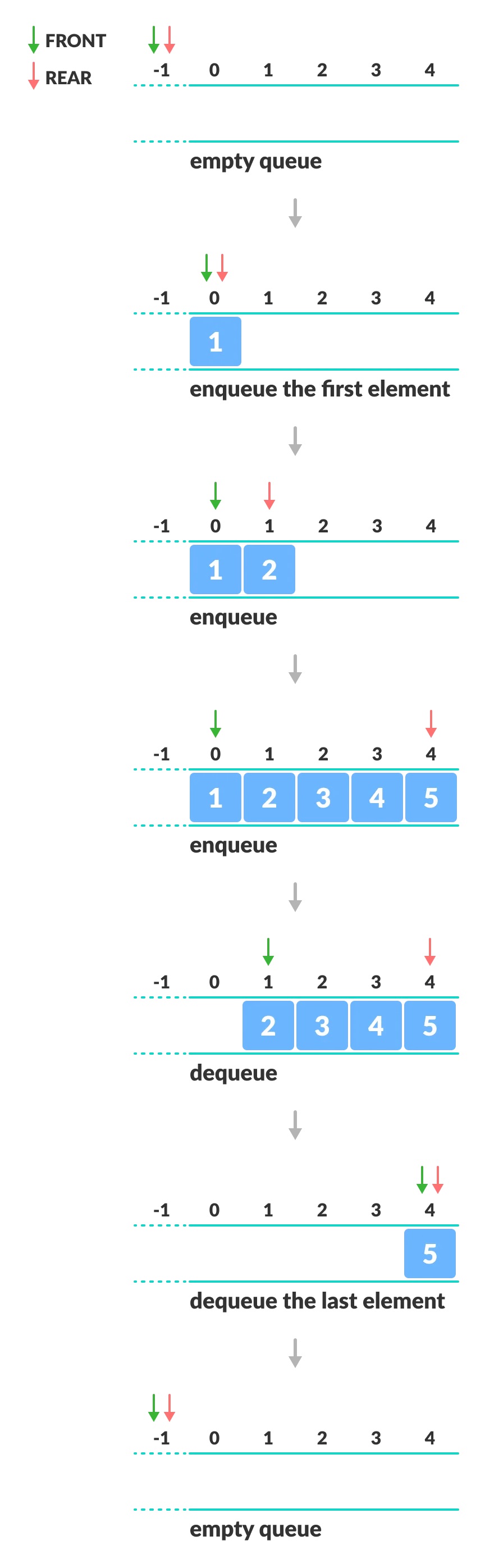
الصورة التالية توضح كيف يتم ذلك: 

لاحظ ان اول عنصر تم إدخاله هو رقم 1 ثم تم ادخال العنصر رقم 2، وبالتالي يتم الوصول الى العنصر رقم 1 أولا. 

العمليات الأساسية Basic Operations

يمكن اجراء العمليات التالية على قوائم الانتظار queue

• Enqueue : أضافة عنصرًا element إلى نهاية قائمة الانتظار
• Dequeue: إزالة عنصر element من مقدمة قائمة الانتظار
• IsEmpty : تحقق من قائمة الانتظار اذا  كانت فارغة.
• IsFull :  تحقق من قائمة الانتظار إذا كانت ممتلئة.
• Peek : الحصول على قيمة اول عنصر element من مقدمة قائمة الانتظار دون حذفه.

كيفية عمل قائمة الانتظار Working of Queue

مثل ما حكينا في بداية الدرس قوائم الانتظار تعمل على مبدأ FIFO لذا لا بد من وجود مؤشرين two pointers. الأول للإشارة الى المقدمة ويسمى FRONT (يشير الى اول عنصر first element في queue)

والثاني للإشارة الى النهاية ويسمى REAR (يشير الى آخر عنصر last element في queue).

يجب في البداية تعيين قيمة -1 لكل مؤشر. 

نفهم العمليات السابقة:

عملية IsEmpty 

يتم في هذه العملية التحقق من قائمة الانتظار إذا كانت فارغة.

طريقة كتابة الخوارزمية تختلف حسب طريقة تطبيق queue. استخدمنا الخوارزمية التالية بسبب استخدام مصفوفة ذات بعد واحد.( يعني لو استخدمنا غير مصفوفة بعد واحد بتكون الخوارزمية غير).

خوارزمية العملية 

procedure isempty
begin
   if (front is less than MIN or less than 0) OR front is greater than rear
      return true
   else
      return false
   endif
end procedure

يتم في هذه الخوارزمية التأكد من قيمة front إذا كانت اقل من min او اقل من صفر. هذا يعني ان queue لا يوجد فيها أي عناصر. وإذا كانت قيمة front اكبر من rear هذا يعني ان جميع القيم تم خروجها من queue وبالتالي تكون فارغة. 

مثال لغة C 

bool isempty() {
   if(front < 0 || front > rear) 
      return true;
   else
      return false;
}

عملية IsFull 

تستخدم للتحقق من قائمة الانتظار إذا كانت ممتلئة.

نفس الكلام السابق بسب استخدام مصفوفة ذات بعد واحد بكون شكل الخوارزمية كالتالي: 

procedure isfull
begin
   if rear equals to MAXSIZE
      return true
   else
      return false
   endif
   
end procedure

في هذه الخوارزمية يتم التحقق من قيمة المؤشر rear في حال الوصول الى قيمة MAXSIZE. عند الوصول الى هذه القيمة هذا يعني ان queue ممتلئ. 

اكيد إذا استخدامنا circular linked-list مع queue بكون شكل الخوارزمية مختلف. 

كود لغة C 

bool isfull() {
   if(rear == MAXSIZE - 1)
      return true;
   else
      return false;
}

لاحظ في الكود استخدمنا السطر 

   if(rear == MAXSIZE - 1)

السبب ان المصفوفة ذات بعد واحد. يعني اخر عنصر فيها بكون في index رقم MAXSIZE – 1 لان البداية تكون من صفر 

عملية Peek 

تستخدم هذه العملية للحصول على قيمة اول عنصر element من مقدمة قائمة الانتظار Queue دون حذفه.

خوارزمية هذه العملية:

procedure peek
begin
   return queue[front]
end procedure

كود لغة C 

int peek() {
   return queue[front];
}

عملية الإضافة Enqueue Operation

لإجراء عملية الإضافة لا بد من التحقق من مجموعة من النقاط:

• تحقق مما إذا كانت queue ممتلئة full
• إذا كانت قائمة الانتظار ممتلئة، ينتج خطأ تجاوز السعة overflow error ومن ثم الخروج.
• اذا كان queue فارغ ضبط قيمة العنصر الأول first element بقيمة 0 (قيمة FRONT تساوي 0)
• زيادة مؤشر REAR بمقدار 1 بهدف الوصول الى المكان الفارغ التالي 
• أضف العنصر الجديد في الموضع المشار إليه بواسطة REAR
• ارجاع تم الإضافة بنجاح.

خوارزمية عملية الاضافة 

procedure enqueue(data)      
   begin
   if queue is full
      return overflow
   endif   
   rear ← rear + 1
   queue[rear] ← data
   return true
end procedure

كود لغة C 

int enqueue(int data)      
   if(isfull())
      return 0;
   rear = rear + 1;
   queue[rear] = data;
   return 1;
end procedure

عملة الحذف Dequeue Operation

لإجراء عملية الحذف لا بد من التحقق من مجموعة من النقاط:

• تحقق مما إذا كانت قائمة الانتظار queue فارغة empty
• إذا كانت قائمة الانتظار queue فارغة، ينتج خطأ underflow error ومن ثم الخروج.
• إرجاع القيمة التي يشير  إليها FRONT (السبب لان العنصر الأول هو الذي سيتم حذفه)
• قم بزيادة مؤشر FRONT بمقدار 1 ليضبح يشير الى العنصر التالي
• ارجاع تم الحذف بنجاح.

خوارزمية الحذف:

procedure dequeue
   begin
   if queue is empty
      return underflow
   end if
   data = queue[front]
   front ← front + 1
   return true
end procedure

كود C

int dequeue() {
   if(isempty())
      return 0;
   int data = queue[front];
   front = front + 1;
   return data;
}

أضف الكود التالي في ملف Notepad ثم أضف اسم مناسب للملف (ليكن queue.c)

ثم نفذ الكود باستخدام command prompt 

// Queue implementation in C
#include <stdio.h>
#define SIZE 5
void enQueue(int);
void deQueue();
void display();
int items[SIZE], front = -1, rear = -1;
int main() {
  //deQueue is not possible on empty queue
  deQueue();
  //enQueue 5 elements
  enQueue(1);
  enQueue(2);
  enQueue(3);
  enQueue(4);
  enQueue(5);
  // 6th element can't be added to because the queue is full
  enQueue(6);
  display();
  //deQueue removes element entered first i.e. 1
  deQueue();
  //Now we have just 4 elements
  display();
  return 0;
}
void enQueue(int value) {
  if (rear == SIZE - 1)
    printf("\nQueue is Full!!");
  else {
    if (front == -1)
      front = 0;
    rear++;
    items[rear] = value;
    printf("\nInserted -> %d", value);
  }
}
void deQueue() {
  if (front == -1)
    printf("\nQueue is Empty!!");
  else {
    printf("\nDeleted : %d", items[front]);
    front++;
    if (front > rear)
      front = rear = -1;
  }
}
// Function to print the queue
void display() {
  if (rear == -1)
    printf("\nQueue is Empty!!!");
  else {
    int i;
    printf("\nQueue elements are:\n");
    for (i = front; i <= rear; i++)
      printf("%d  ", items[i]);
  }
  printf("\n");
}

حدود قائمة الانتظار Limitations of Queue

حكينا في بداية الدرس عن استخدام المصفوفات وحكينا من مساوئه المحدودية.  لاحظ الصورة التالية :

واضح من الصورة عندنا امكان فارغة وهي (0 و 1) ولا يمكن إعادة استخدامها بالطريقة التقليدية. 

طبعا هذه النتيجة (الصورة السابقة) حصلنا عليها بعد اجراء مجموعة من عمليات الإضافة والحذف. ولان queue بتشتغل على مبدأ FIFO لا يمكن إعادة استخدام هذه الأماكن الفارغة الا بعد عمل إعادة تعيين. إعادة الترتيب يعني الغاء ترتيب جميع العناصر. 

لحل هذه المشكلة نستخدم circular queue

تحليل التعقيد Complexity Analysis

تعقيد عمليات الإضافة enqueue والحذف dequeue في قائمة الانتظار باستخدام مصفوفة هو 

O(1)

إذا كنت تستخدم pop(N) في كود البرمجي، هذا يعني ان التعقيد هو

 O(n) 

اعتمادًا على موضع العنصر المراد ظهوره.

تطبيقات على قوائم الانتظار Applications of Queue

• CPU scheduling
• Disk Scheduling

عندما يتم نقل البيانات بشكل غير متزامن asynchronously بين عمليتين ، يتم استخدام قائمة الانتظار  queue للمزامنة. على سبيل المثال: IO Buffers ، pipes، file IO، إلخ

من الأمثلة على ذلك 

تستخدم أنظمة الهاتف في مركز الاتصال Call Center قوائم الانتظار لإبقاء الأشخاص الذين يتصلون بها بالترتيب.